頑丈なスケジュールはこうやって組み立てる 〜 イチから作る同人CDの裏方仕事(4)

2週間ぶりです。どうも、餅屋です。

2週間お休みをいただいて、紅楼夢の生産作業や諸対応、M3や京都秘封の準備に追われておりました。身体があと二つほしいですし、おいしい肉とか食べに行きたいところです。

今回のお話に移る前に「2016/10/09 東方紅楼夢12」では「た-24b」にスペースを構えております。新譜も用意しておりますので是非、足をお運びください。

さて前回に引き続き今回も耳が痛いスケジュールのお話です。といっても、今回の話はかなり難しい話になり、私もちゃんと説明できているかどうかかなり不安な内容になります。

ですが、できる限りわかりやすく解説できるように心がけましたので、お付き合いいただきたく思います。それでは今週も宜しくお願い致します。

スケジュールを組み立てる

前回は工程に内包される作業の数の把握と一つの作業あたりにかかる時間の書き出しを行いました。それぞれ一工程を分解し一作業にかかる時間を把握、それに基づいて工程全体の流れと時間を把握することが容易となりました。

ここからは、正確なスケジュールを組み立てるために以下の段階を踏まえてスケジュールを組んでいきたいと思います。まず今回のお話をさせて頂くにあたり、以下の内容でCDを作成するという事を前提にお話をさせていただきます。

• 30日後のイベントに参加するためにCDを1枚作成する
• 指定の宅配便の集荷基地には26日に必着である
• 集荷基地には自宅から発送して到着まで最短1日かかるものとする
• 企画を出し、参加者を募るのに最短２日かかる。
• 曲を作成し2mixが完成するまで最短8日かかる
• イラストを依頼し完成するまで最短６日かかる
• すべての資材を発注して届くまで最短４日かかる
• マスタリングしてもらうのに最短３日かかる
• ジャケットをデザインする最短２日かかる
• ＣＤのラベルを印刷するのに最短２日かかる
• ＣＤをライティングするのに最短２日かかる
• ジャケットを印刷所に入稿し納品されるのに最短３日かかる
• ＣＤを組み立てするのに最短１日かかる

これらの工程を直列にして作業をしようとすると単純計算で30日ほどかかる試算になります。直列で作業し宅配搬入をせず直接搬入をすれば、イベント当日にぎりぎり間に合うか間に合わないかの計算になりますが、どこか一日遅れてしまえば途端に間に合いません。

これは極端な例となりますが、馬鹿正直に工程を直列に並べて作業する方はほとんどいらっしゃらないでしょう。同時進行で作業を進めるシーンがもちろん存在するはずです。それらを加味して実際に作業を行うなら、という形で作業を並べていきます。

作業に前提条件を付けていく。

とはいっても実際に作業を行うとしてどうやって順番を決めていけば良いのかというお話になります。そこで作業を行う上で「前提条件」をつけて組み立てていきます。

例えば、うどんを作るのに「出汁」と「うどん」と「具」ができていないといけません。その「うどん」を作るのに「うどんが茹でてあること」や「うどんが完成していること」、「うどん粉」が練れている事など、各作業が元を辿っていくと数々の作業が完了している事が前提で成り立っていることが分かります。

それと同じ要領で最後から数えた時に、CDを完成させるにはどんな作業を終えていなければならないかを逆算的に考えて工程や作業の順番を決めていきます。

今回の作業を行うにあたり、前提条件はこのように設定されます。

このようにどの作業が終わっていないと次の作業に移れないのかを明確化することによって、前提となる作業を把握する事が容易になりました。

アローダイアグラム(順番の可視化と、余裕日数・最大遅延日数の把握)

しかし、文字に書き出しただけでまだまだ分かりづらい状態になります。今度はそれらの順番を把握するために「アローダイアグラム」というフォーマットで流れを図式化したいと思います。

この「アローダイアグラム」はネットワーク図の一種になり、プロジェクトを構成する各工程の依存関係（前の工程が完了しないと、次の工程に移れない）に基づいてそれらを矢印で繋いでいく手法になります。これを行う事により、工程ごとの依存関係の把握や工程ごとに必要な所要日数(必要な日数)・最大遅延日数(最大どれだけ遅延できるのか)・余裕日数(何日余裕があるのか)などを把握することができます。これらを用いて、プロジェクト全体に必要な日数を見積もる事ができるフォーマットになります。

先ほど前提条件を書き入れた作業内容をアローダイアグラムに落とし込んでみましょう。

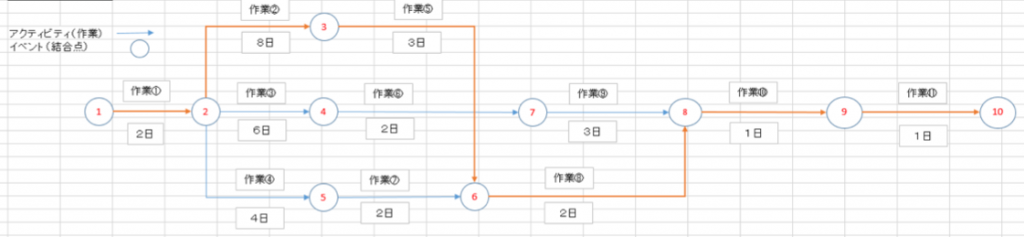
図に書いてありますが、矢印が「アクティビティ(作業)」、丸に数字が入っているものが「イベント(結合点)」となります。矢印のおしりから先端に向かって作業が進んでいき、それぞれのおしりについているイベントが先端のイベントに向かって進んでいきます。

この矢印が先ほど書き出した「作業」であり次のイベントに進むにはこの「作業」を完了しなければ次のイベントに進めません。このように関連性のあるアクティビティをチェックポイントであるイベントを同士でつないでスタートからゴールまで進む図を作成する形になります。この「アローダイアグラム」を作るうえで下記のようなルールがございます。

1. スタートとゴールを例外に全てのイベントは前後にイベントを持つ
2. イベントとイベントは関連性のあるアクティビティで接続されている
3. 後続のイベントは前のイベントに書かれている数字より大きくなる
4. アクティビティが二つ接続されているイベントは全て終わらないと次のアクティビティに移ることができない
5. 前のイベントに戻ることはできない。

そのほかルールがございますが、それは各自でググってください。これらのルールに基づいてアローダイアグラムを形成していきましょう。

最大遅延日数と余裕日数の把握

アローダイアグラムを使うにあたってもう一つの利点があるのは、前項で簡単に説明したと思います。今度はそのもう一つの利点である「遅延できる日数」と「どれだけ余裕があるのか」を計算していきます。

まずここで覚えてもらいたいのは下記のワードになります。

最早結合点：アクティビティごとに一番早く実施することができる日数。

計算方法はイベントの数が小さい方から作業ごとにかかる日数を足していく。

（イベント①はスタート地点なので0日からスタートできる。イベント②は作業①にかかる日数が2日である為0+2=2日からスタートできる、というように前の日数をどんどん足し算していく。分岐して合流する場合はそこに到達するまで一番日数が多い日を記入する）

最遅結合点：次の作業開始までのタイムリミット

計算方法はイベントの数が大きい方から締切の日数を引いていく。

(締切が26日なのでそこから作業⑪を引くと26-1＝25日となり、作業ごとにどんどん日数を引いていく。分岐して合流する場合はそこに到達するまで一番日数が少ない日を記入する)

余裕日数：その作業を開始するまでにどれだけ余裕があるか

計算方法は各作業の「最遅結合点」－「最早結合点」となる。

(最遅結合点が10日で最早結合点が4日なら6日余裕があることになる)

その他余裕日数が0になる経路をクリティカルパス（遅れる事ができない経路）とかありますが、ここでは割愛します。この説明では別に気にしなくても死にはしません。

作業にかかる日数を入れていくとこのような図が出来上がります。

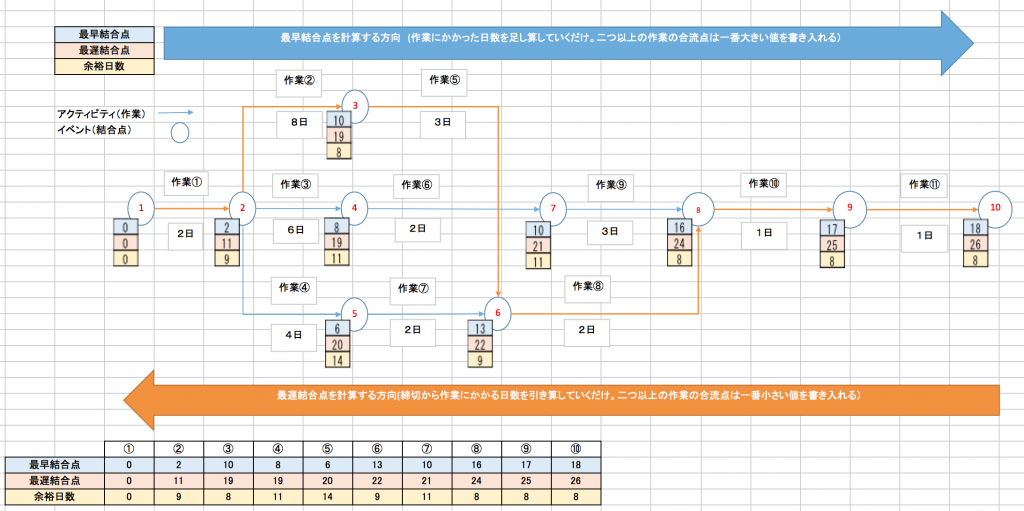
どの作業をどの順番で作業し、どれだけ時間が必要なのか。またいつまでに作業を開始しなくてはならなくて、その作業にどれだけ余裕があるのかをいっぺんに可視化することが可能となります。より確実性のあるスケジュールの見積もりを立てる際には、「アローダイアグラム」は非常に利便性の良いフォーマットになります。

ここまでの話

正直な話をしますと今回の話は非常に難しい内容となり、面倒くさい内容となりますが作業の順番の把握や日数の把握、どれだけ余裕があるのかを予め見積もりを立てておくことにより作業にゆとりをもたらすことができますので、ぜひ一度やっていただきたい内容となりました。

さて前回・今回と引き続き次回もスケジュールの話となります。いよいよ今度はスケジュールを表にして「ちゃんと使える形」に起こしていきます。かなり長い内容となりましたが、次回でスケジュール編はラストになります。この一連の下準備が終わりましたら、次はいよいよ実技の予定です。

が、その前に秋のイベントシーズンですのでイベントにまつわるお話をするかもしれません。それでは次回もよろしくお願いします。